因果知识入门(一) #
What if I had done…? Why? #
结果因果模型 Structural Causal Model #
概述 #
结构因果模型描述了为感兴趣的变量赋值的方法,从形式上来看,结构因果模型含有两个变量集$U$和$V$和一组函数:
$$
f={f_X:W_X\rightarrow X \ |\ X \in V}
$$
其中$W_X\subseteq(U \cup V)-\{X\}$,$U$为外生变量,$V$为内生变量,内生变量至少为一个外生变量的后代。由此,因果可以定义为:
(1)若$Y$存在于$f$的定义域中,则$Y$为$X$的直接原因。
(2)若$Y$是$X$的直接原因或原因的原因,则$Y$是$X$的原因。
以外生变量为根节点,可以构建表示变量关系的有向无环图,即结构因果模型。在结果因果模型中,父母节点是其子节点的直接原因,是其后代的潜在原因。
乘积分解法则 #
$$ P(x_1,x_2,···\ ,x_n)=\prod_{i}P(x_i\ |\ pa_i) $$
$pa_i$表示变量$x_i$的所有父节点。乘积分解法则可以实现分类单元的分解,达到更准确的估计。当然,也存在特殊的非传递依赖情形,子节点取值独立于父节点。
图模型的应用 #
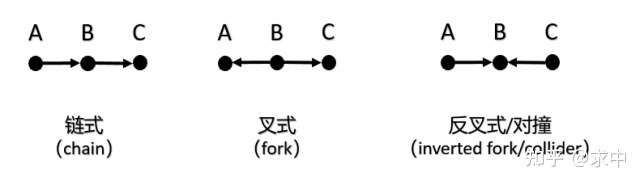
链结构及其条件独立性 #
如果变量$A$和$C$之间只有一条单向路径,$B$是截断这条路径的任何一组变量,则在给定$B$的条件下,$A$和$C$独立。
叉式结构及其条件独立性 #
如果变量$B$是变量$A$和变量$C$的共同原因,并且$A$和$C$之间只 有一条路径,则$A$和$C$在给定$B$的条件下独立。中间节点$B$常被视为$A$和$C$的共因(common cause)或混杂因子(confounder)。
对撞结构及其条件独立性 #
图中的对撞结构表示两个原因$A$和$B$的共同效应$B$,$A$和$C$在$B$的条件下可能是相互依赖的,举例而言,若获得奖学金的必要条件为学习优秀或体育出众,则如果已知获得奖学金并且体育不出众,那么一定可以推出学习优秀。即固定两个独立变量的共同效应的值时,这两个独立变量可能会变得相互依赖。
即,如果变量$B$是变量$A$和变量$C$之间的对撞节点,并且$A$与$B$之间只有一条路径,那么$A$与$C$之间无条件独立,但是在$B$或$B$的任何子孙条件下是相互依赖的。
d-分离 d-separation #
大多数实际图模型中,变量之间可能有多条路径连接,且每条路径包含多个上述结构。在这种背景下,d-分离方法可用于判断任何一对节点之间是否存在连通路径(即d-连通),若不存在连通路径,则称这一对节点为d-分离。d-分离的两个变量绝对独立,d-连通的两个变量很有可能相互依赖。
d-分离分为如下两类:
(1)**不以任何节点为条件,,只有对撞节点可以阻断一条路径,**因此,如果两个节点$A$和$B$之间的每条路径上都有对撞节点,则$A$和$B$不会有依赖关系。
(2)以一组节点$Z$为条件,以下类型的节点可以阻断一条路径
自身不在
$Z$中且其子孙节点也不在$Z$中的对撞节点。在
$Z$中的链节点或分叉结构的中间节点。如果
$Z$阻断了$X$和$Y$间的每一条路径,则$X$和$Y$在$Z$的条件下是d-分离的,$X$和$Y$在$Z$的条件下独立。
d-分离是一种非参数的检验模型的方法,它不依赖于任何具体的变量间的函数,仅仅使用问题中的图模型;同时,它可以实施局部性的检验,即使无法确定模型某个区域的参数,也可以识别假设模型中有缺陷的特定区域并修复。
干预 #
干预的含义 #
对一个变量进行干预和以该变量为条件具有明显的区别。当以一个变量为条件时,我们不做任何改变,仅仅关注问题的子集。因此,以变量为条件改变的是我们对世界的看法,而不是世界本身;而当干预模型中的一个变量时,固定这个变量的值意味着改变了系统,削弱了该变量为响应其他变量而变化的自然趋势,这相当于在图模型上删除指向该变量的所有边。
区分变量$X$自然取值$x$和固定$X$取值$x$的符号区分,后者用$do(X=x)$来表示。$P(Y=y|X=x)$反映了$X$取值为$x$的个体在$Y$上的总体分布,而$P(Y=y|do(X=x))$反映了如果群体中每个个体均将$X$固定为$x$时,$Y$的总体分布。两种形式可以组合,如$P(Y=y|do(X=x),Z=z)$表示对于给定的$Z=z$,干预$do(X=x)$得到分布中$Y=y$的条件概率。
校正公式* #
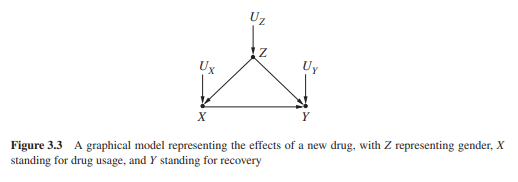
$X$代表使用药物,$Y$代表痊愈,$Z$代表性别,$Z$和$X$都对$Y$有影响。为了确定药物在人群中的有效性,设想一种假设性的干预措施,即对整个人群统一服用药物,并与补充干预下的痊愈率进行比较(补充干预指阻止每个人服用药物),用$do(X=1)$表示第一种干预,$do(X=0)$表示第二种干预,则两种干预的差异为:
$$
P(Y=1|do(X=1))-P(Y=1|do(X=0))
$$
该差异称为平均因果效应(ACE, average causal effect)。一般地,如果$X$和$Y$都能取多个值,则希望$x$和$y$取遍所有可能取得的值来预测综合因果效应 $P(Y=y | do(X=x))$。
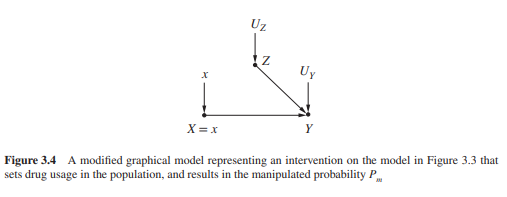
为此,对图进行处理以模拟干预:
因果效应 $P(Y=y | do(X=x))$ 与图中修改后模型的条件概率 $P_m(Y=y | X=x)$ 相等。 $P_m$ 代表修改后模型中的概率,也被称为操纵概率,操纵概率具有两个基本属性:
(1)边缘概率 $P(Z=z)$ 在干预前后不变,本例中意味着干预前后男女患者的比例不变。
(2)条件概率 $P(Y=y|Z=z,X=x)$ 不变,因为不管$X$自发变化还是被操纵发生变化,$Y$对$X$和$Z$的响应函数$Y=f(x,z,u_Y)$不变。
由此得到两个不变性方程: $$ P_m(Y=y|Z=z,X=x)=P(Y=y|Z=z,X=x) $$
$$ P_m(Z=z)=P(Z=z) $$
因$Z$和$X$在修改后的模型中d-分离,因此在干预分布中是独立的,即$P(Z=z|X=x)=P_m(Z=z)=P(Z=z)$。综上,由全概率公式可以得到:
$$
P(Y=Y|do(X=x))=P_m(Y=y|X=x)(由定义)=\sum_zP_m(Y=y|X=x,Z=z)P_m(Z=z|X=x)=\sum_zP_m(Y=y|X=x,Z=z)P_m(Z=z)(本例Z和X独立)
$$
即以$Z=z$ 的所有值为条件求条件概率后求和 。利用不变性关系,得到一个以干预前概率表示的因果效应公式:
$$
P(Y=y|do(X=x))=\sum_zP(Y=y|X=x,Z=z)P(Z=z)
$$
上式即为校正公式(adjustment formula),它对每一个$Z$的值$z$计算了$X$和$Y$之间的关系,并对这些值求了平均值,此过程 称为“对$Z$的校正”(adjusting for Z) 或者“对Z的控制”(controlling for Z)。
最后一次修改于 2022-11-22